About
I'm a financial economist working on empirical asset pricing and financial intermediation, often using text as data. Here you can learn a bit more about my work.
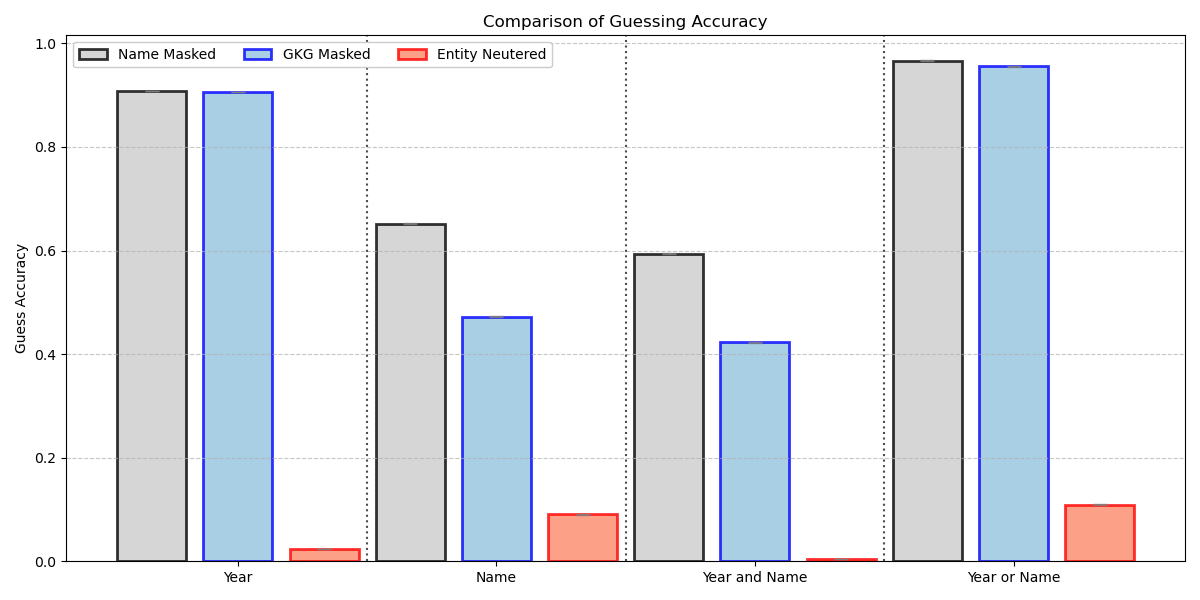
LLM guessing accuracy by de-identification method
This figure is from a recent paper titled Entity Neutering. Cutting-edge LLMs are trained on recent data, creating a concern about look-ahead bias. We propose a simple solution called entity neutering: using the LLM to find and remove all identifying information from text. In a sample of one million financial news articles, we verify that, after neutering, ChatGPT and other LLMs cannot recognize the firm or the time period for about 90% of the articles. Among these articles, the sentiment extracted from the raw text and the neutered text agree 90% of the time and have similar return predictability, with the difference providing an upper bound on look-ahead bias. The evidence here suggests that LLMs are able to effectively neuter text while maintaining semantic content. For look-ahead bias, LLMs can be both the problem and the solution.
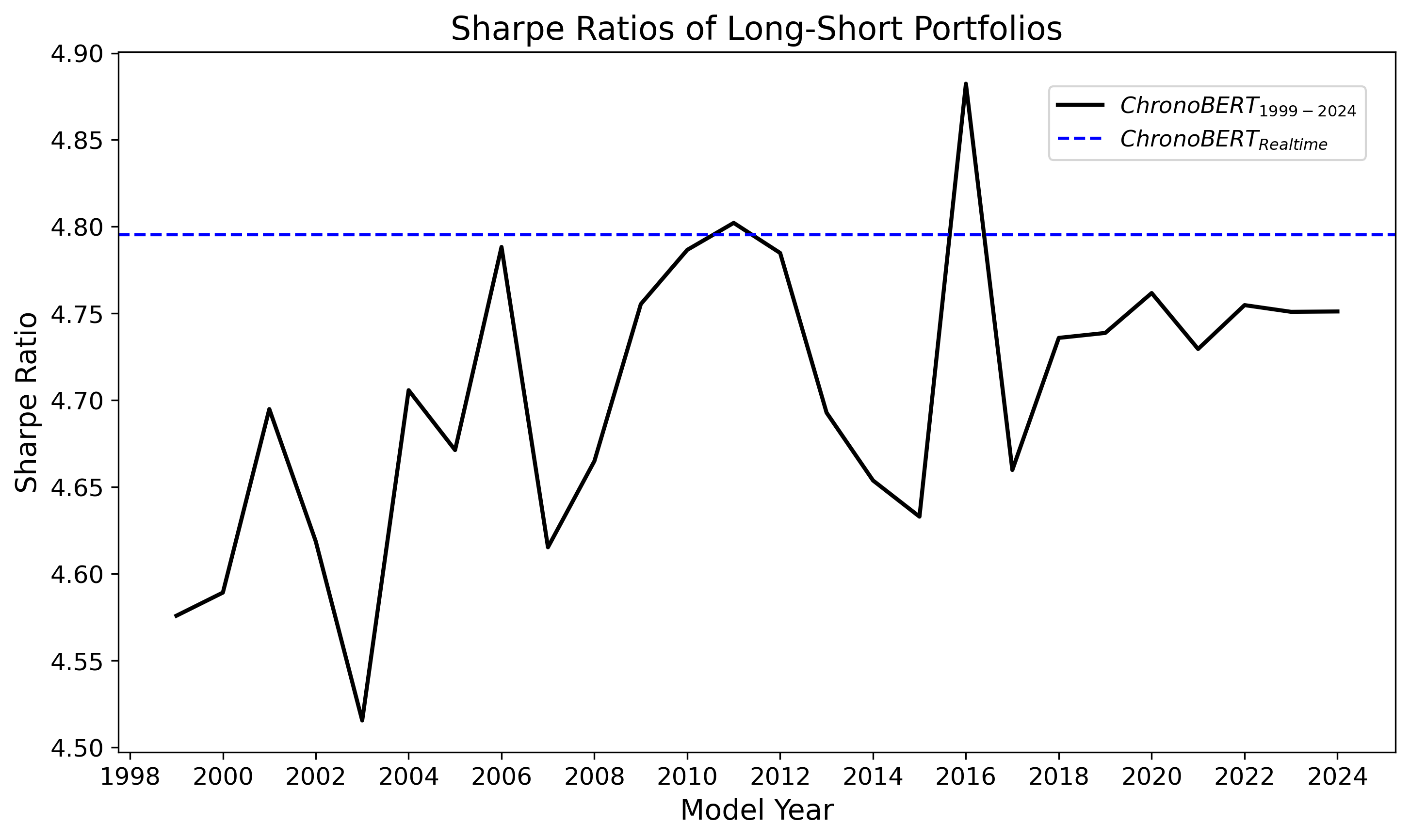
Sharpe ratios of long-short portfolios across large language model vintage
This figure is from a recent paper titled Chronologically Consistent Large Language Models. Large language models are increasingly used in social sciences, but their training data can introduce lookahead bias and training leakage. A good chronologically consistent language model requires efficient use of training data to maintain accuracy despite time-restricted data. Here, we overcome this challenge by training chronologically consistent large language models timestamped with the availability date of their training data, yet accurate enough that their performance is comparable to state-of-the-art open-weight models. Lookahead bias is model and application-specific because even if a chronologically consistent language model has poorer language comprehension, a regression or prediction model applied on top of the language model can compensate. In an asset pricing application, we compare the performance of news-based portfolio strategies that rely on chronologically consistent versus biased language models and estimate a modest lookahead bias.